Just a reminder of what these mean.
Dot Product
Dot product is a scalar magnitude. You take the X components of both and multiply them together, and take the Y components of both and multiply them together, and then add those.

Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates.
The Cross Product
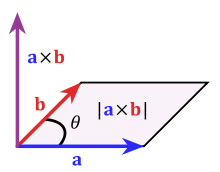
The cross product a × b is defined as a vector c that is perpendicular (orthogonal) to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.